The Theodorus Spiral Company is part of a multi-media, multi-access creative installation.
The pursuit of the maths and patterns of the spiral is genuine.
I first learnt about the Theodorus Spiral when I was reading An Imaginary Tale: The Story of The Square Root of -1 by Paul Nahin (1998). Each hypotenuse (longest side of the triangle) or spoke is always longer than the one before as the spiral goes around, but the difference in the change of length is getting smaller and smaller. The angle between the spokes is getting smaller and smaller while the angle between the opposite and adjacent side is always a right angle.
I had been training as an artistic blacksmith since 2006 and after seeing the theodorus spiral (on page 33 of Paul’s book) I thought of the idea to make an iron shield in the shape of the spiral. My intention was that it would be a work of art rather than a practical shield. This has evolved into a sculpture titled My Painted Elephant: Part 3: Kembla’s work; called a Monument to Hypatia. The Theodorus Spiral on the Pedastal is part of that sculpture and is featured in my novella; A Perpetual Tale to be found on my website The Red Forge Publishing House.
I also began investigating the maths of the spiral. I was learning to use Matlab and began playing with some code I had written to see what happens to the spiral at a very large x. I thought it was converging into a circle but it expands even though the change in the hypotenuse gets smaller and smaller. What is the change in the circumference of the circles? Why is the difference between the winding’s gets closer and closer to pi!
I began to ponder all these plus more of the following Theodorus Spiral mathematical and data visualisation questions:
-
what is the change in the hypotenuse and the change in the change of the hypotenuse?
-
what is the change in the angles and the change in the change of the angles
-
how far does it go?
-
what about 0 < x <1 and x < 0?
-
what would a 3D model look like?
-
how many spokes in each winding? It seems that the additional number of spokes in each winding is between 18 and 21 in a seemingly random pattern. I have begun calling this the Theodorus Spiral Winding Pattern and I am going to start looking for this pattern in other places.
x=1000
MATLAB CODE by Keren Sutcliffe
Created by Keren Sutcliffe 2011
clear all
%finish = 16 creates the spiral that Theodorus completed
%change the value of finish to any number
total_angle=0; winding=0; finish=16;
fprintf(‘ x hyp changeinhyp chngeinchngehyp angle chngeangle X2 Y2 winding \n’);
for x=1:finish
hyp=sqrt(x+1); chngeinhyp=1/(2*sqrt(x+1));
chngechngehyp=1/(-4*sqrt(x+1));
angle=atan(1/sqrt(x));
degangle=angle*180/pi;
chngeangle=(1/(1+x))*(1/(2*sqrt(x)));
total_angle=total_angle+angle;
degtotal_angle=total_angle*180/pi;
X=hyp*cos(total_angle);
Y=hyp*sin(total_angle);
winding=degtotal_angle/360;
%outside boundry
Xb=hypb*cos(total_angle-angle);
Yb=hypb*sin(total_angle-angle);
fprintf(‘%3i %10f %10f %10f %10f %10f %10f %10f %5f \n’,x,hyp,chngeinhyp,chngechngehyp,degangle,chngeangle,X,Y,winding);
figure(1) title(‘Theodorus Spiral’) axis equal; xlabel (‘x’); ylabel (‘y’); zlabel (‘z’);
hold on
plot ([0 1], [0 0],‘k’); %First spoke
plot ([0 X],[0 Y],‘k’); %spokes
plot ([Xb,X],[Yb Y],‘k’); %boundary on xy grid
end
x hyp changeinhyp chngeinchngehyp angle chngeangle X Y winding 1 1.414214 0.353553 -0.176777 45.000000 0.250000 1.000000 1.000000 0.125000 2 1.732051 0.288675 -0.144338 35.264390 0.117851 0.292893 1.707107 0.222957 3 2.000000 0.250000 -0.125000 30.000000 0.072169 -0.692705 1.876209 0.306290 4 2.236068 0.223607 -0.111803 26.565051 0.050000 -1.630810 1.529856 0.380082 5 2.449490 0.204124 -0.102062 24.094843 0.037268 -2.314982 0.800536 0.447012 6 2.645751 0.188982 -0.094491 22.207654 0.029161 -2.641800 -0.144552 0.508700 7 2.828427 0.176777 -0.088388 20.704811 0.023623 -2.587164 -1.143058 0.566213 8 3.000000 0.166667 -0.083333 19.471221 0.019642 -2.183032 -2.057759 0.620300 9 3.162278 0.158114 -0.079057 18.434949 0.016667 -1.497113 -2.785436 0.671508 10 3.316625 0.150756 -0.075378 17.548401 0.014374 -0.616280 -3.258865 0.720254 11 3.464102 0.144338 -0.072169 16.778655 0.012563 0.366304 -3.444680 0.766861 12 3.605551 0.138675 -0.069338 16.102114 0.011103 1.360698 -3.338937 0.811589 13 3.741657 0.133631 -0.066815 15.501360 0.009905 2.286752 -2.961547 0.854648 14 3.872983 0.129099 -0.064550 14.963217 0.008909 3.078259 -2.350387 0.896213 15 4.000000 0.125000 -0.062500 14.477512 0.008069 3.685127 -1.555584 0.936428 16 4.123106 0.121268 -0.060634 14.036243 0.007353 4.074023 -0.634302 0.975418
Different variations of basic code
Overlapping: Apparently according to Wikipedia, in 1958, Erich Teuffel proved that no two hypotenuses will ever coincide, regardless of how far the spiral is continued. I haven’t seen this proof. If it doesn’t overlap I wonder what it would look watching, from the origin, the plot of points as the spiral winds. What is that pattern and is there a formula?
Also if the Theodorus Spiral goes on into infinity and the spokes never overlap, is this significant for computer science and information storage? I mean in terms of pointers and list/arrays/stacks or ‘theodorus positioning’???
Learn Maths and Computer Programming with the Theodorus Spiral
Theodorus Spiral Trinket Matlab picture, 3D print
and inside the VOXON
Theodorus Spiral: Cup and Saucer (2015) by K E Sutcliffe: Coloured cup and saucer with inner piece (created in Matlab)
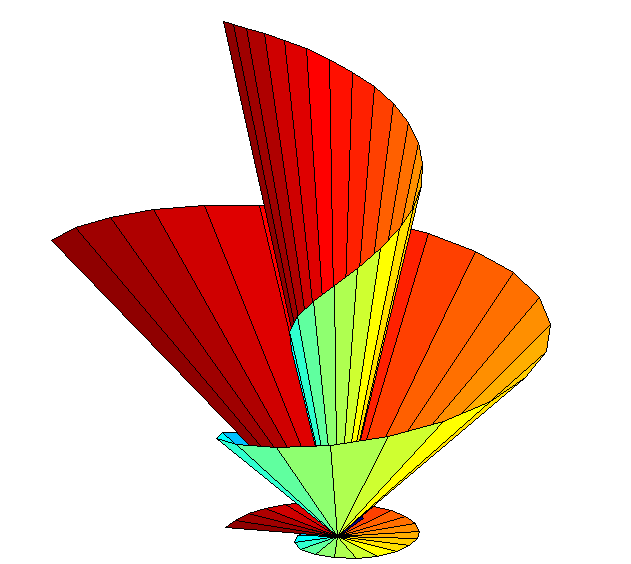
3D Theodorus Spirals (2016)by K E Sutcliffe: Two spirals at right angles to each other (created in Matlab)
Theodorus Spiral on the Pedestal @ The Port Festival 2015
Two Brains – new Matlab Theodorus Spiral design by K E Sutcliffe (2017)
Design Mashup (2017)
More than one spiral on one figure.
The Blades (2017) Something a bit different: starting with negative numbers.
Something a bit different: starting with negative numbers.
Theodorus Spiral: Cover of The Wave and the Particle (A novel by Keren Sutcliffe)

Theodorus Spiral Company Merchandise Store
Theodorus Spiral Company Colouring In
References
Wikipedia – Spiral of Theodorus
Further Reading
Gronau, D. The Spiral of Theodorus www.uni-graz.at/~gronau/monthly230-237.pdf
Hlawka (Gleichverteilung und Quadratwurzelschnecke, Monatsh. Math., 89 (1980) 19-44)
Kociemba, H (2014) Die Wurzelspirale
Theaetetus by Plato
Theodorus of Cyrene in World Cat
The Red Forge Publishing House
home of A Perpetual Tale
by Keren Sutcliffe



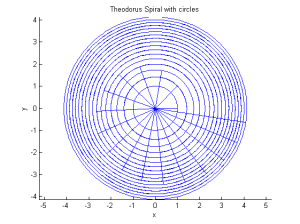
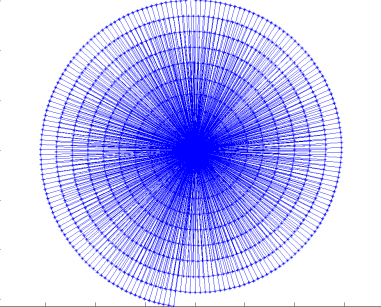






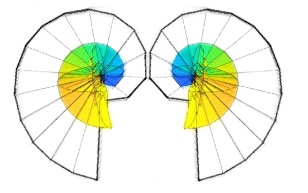
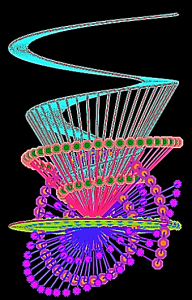
 Positive and Negative FlareUp
Positive and Negative FlareUp
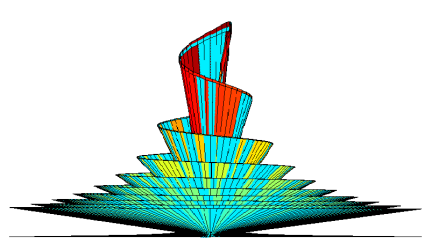







Just wish to say your article is as astonishing.
The clarity in your post is just great and i could assume you’re an expert on this
subject. Well with your permission allow me to grab
your RSS feed to keep updated with forthcoming post.
Thanks a million and please carry on the gratifying work.
LikeLiked by 1 person
Thank you. Yes, please stay connected. For me; maths, science, technology and can be wonderfully integrated with art and fiction. It helps with the learning process and advancement of knowledge.
LikeLike